本文共 3159 字,大约阅读时间需要 10 分钟。
节点:
192.168.2.84(主)192.168.2.142(从)
一、主服务器192.168.2.84
1、登陆主服务器192.168.2.84
[root@youyun-284 mysql]# mysql -uroot -p
2、创建一个专门为复制服务的用户
CREATE USER 'repl'@'%' IDENTIFIED BY 'xxxxxxxx';
flush privileges;
3、修改my.cnf文件
| server-id = 2 //要求各个服务器的这个id必须不一样 binlog_format = MIXED //binlog日志格式,mysql默认采用statement,建议使用mixed() log-bin = master-a-bin //binlog日志文件名 expire_logs_days = 7 //binlog过期清理时间 max_binlog_size = 100m //binlog每个日志文件大小 binlog_cache_size = 4m //每个session分配的binlog缓存大小,事务提交前产生的日志,记录到Cache中;事务提交后,则把日志持久化到磁盘 max_binlog_cache_size = 512m //最大binlog缓存大小binlog_do_db = pay-order //指定同步数据库实例名,多个数据库实例名需要指定多个 #binlog_do_db = pay-channel |
|---|
4、配置从服务器登录主服务器的账号授权
GRANT REPLICATION SLAVE ON *.* TO 'repl'@'%';
flush privileges;
4、重启mysql
sservice mysqld restart或systemctl restart mysql5、再次登陆192.168.2.84后,查看主服务状态信息
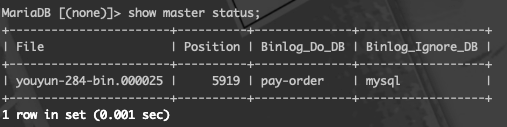
锁表,只读,任何用户都没有写入数据库的权限),待从服务器配置后好,需要解锁表(unlock table)。 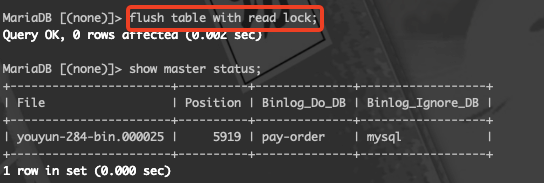
二、从服务器192.168.2.142
7、登陆从服务器192.168.2.142
[root@youyun-284 mysql]# mysql -uroot -p
8、设置该机对应的主服务器信息
mysql> change master to -> master_host='192.168.2.84', -> master_port= 3306, -> master_user='repl', -> master_password='xxxxxxxx', -> master_log_file='youyun-284-bin.000025', -> master_log_pos=5919; |
|---|
属性值解释:
| 属性名 | 描述 |
|---|---|
| master_host | 主服务的ip |
| master_port | 主服务的端口号 |
| master_user/master_password | 从机复制主机的账号与密码 |
| master_log_file | 开始同步复制主机的日志文件名(与主服务的File的值对应,否则同步失败) |
| master_log_pos | 开始同步复制主机的日志文件名的位置标示(与主服务的Position的值对应,否则同步失败) |
9、启动从服务
mysql>start slave;
10、查看从服务状态信息,其中Slave_IO_State 的值为 Waiting for master to send event ,表示已经准备好接受主库发送过来的归档日志进行处理了。
注意:如果这两个参数均为YES,则设置成功:Slave_IO_Running: Yes Slave_SQL_Running: Yes。
| *************************** 1. row *************************** Slave_IO_State: Waiting for master to send event Master_Host: 192.168.2.84 Master_User: root Master_Port: 3306 Connect_Retry: 60 Master_Log_File: youyun-284-bin.000025 Read_Master_Log_Pos: 4067 Relay_Log_File: youyun-2142-relay-bin.000002 Relay_Log_Pos: 560 Relay_Master_Log_File: youyun-284-bin.000025 Slave_IO_Running: Yes Slave_SQL_Running: Yes Replicate_Do_DB: pay-order Replicate_Ignore_DB: Replicate_Do_Table: Replicate_Ignore_Table: Replicate_Wild_Do_Table: Replicate_Wild_Ignore_Table: Last_Errno: 0 Last_Error: Skip_Counter: 0 Exec_Master_Log_Pos: 4067 Relay_Log_Space: 875 Until_Condition: None Until_Log_File: Until_Log_Pos: 0 Master_SSL_Allowed: No Master_SSL_CA_File: Master_SSL_CA_Path: Master_SSL_Cert: Master_SSL_Cipher: Master_SSL_Key: Seconds_Behind_Master: 0 Master_SSL_Verify_Server_Cert: No Last_IO_Errno: 0 Last_IO_Error: Last_SQL_Errno: 0 Last_SQL_Error: Replicate_Ignore_Server_Ids: Master_Server_Id: 1 Master_SSL_Crl: Master_SSL_Crlpath: Using_Gtid: No Gtid_IO_Pos: Replicate_Do_Domain_Ids: Replicate_Ignore_Domain_Ids: Parallel_Mode: conservative SQL_Delay: 0 SQL_Remaining_Delay: NULL Slave_SQL_Running_State: Slave has read all relay log; waiting for the slave I/O thread to update it Slave_DDL_Groups: 7 Slave_Non_Transactional_Groups: 0 Slave_Transactional_Groups: 15 1 row in set (0.00 sec) |
|---|
10、将主机192.168.2.84的主服务的表解锁unlock table.
mysql>unlock table;
11、排查错误
如果出现从服务不同步或同步失败,可以查看从服务的状态信息中的“Last_Error”和“Last_SQL_Error”来排查错误。

参考文章:
转载地址:http://hlxhz.baihongyu.com/